Solved

Match the Logistic Differential Equation and Initial Condition with the Graph

Question 11

Multiple Choice

Match the logistic differential equation and initial condition with the graph of its solution shown below. ​ Match the logistic differential equation and initial condition with the graph of its solution shown below. ​ ​ A) B) C) D) E) ​


A) Match the logistic differential equation and initial condition with the graph of its solution shown below. ​ ​ A) B) C) D) E)
B) Match the logistic differential equation and initial condition with the graph of its solution shown below. ​ ​ A) B) C) D) E)
C) Match the logistic differential equation and initial condition with the graph of its solution shown below. ​ ​ A) B) C) D) E)
D) Match the logistic differential equation and initial condition with the graph of its solution shown below. ​ ​ A) B) C) D) E)
E) Match the logistic differential equation and initial condition with the graph of its solution shown below. ​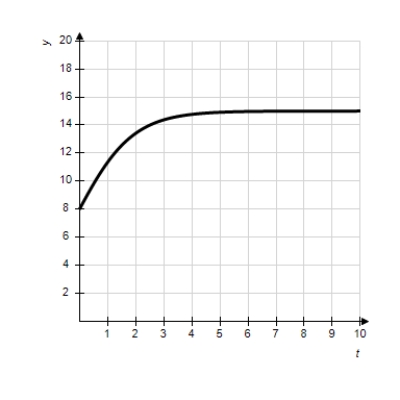 ​ A) 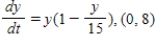B) 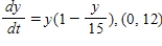C) 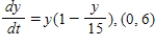D) 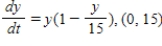E)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q6: The logistic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="The logistic

Q7: Sketch a few solutions of the differential

Q8: Use Euler's Method to make a table

Q9: The initial investment in a savings account

Q10: The logistic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="The logistic

Q12: Use integration to find a general solution

Q13: Sketch a few solutions of the differential

Q14: Find the general solution of the differential

Q15: A 300-gallon tank is half full of

Q16: Solve the differential equation. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"