Solved

Write and Solve the Differential Equation That Models the Following

Question 23

Multiple Choice

Write and solve the differential equation that models the following verbal statement: ​
The rate of change of Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) , with respect to Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) , is proportional to Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) , .
​


A) Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) , , Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) ,
B) Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) , , Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) ,
C) Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) , , Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) ,
D) Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) , , Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) ,
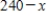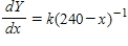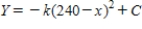
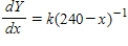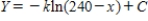
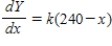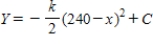
E) Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) , E) , , Write and solve the differential equation that models the following verbal statement: ​ The rate of change of with respect to is proportional to . ​ A) , B) , C) , D) 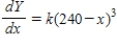, E) ,

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q18: Find the orthogonal trajectories of the family

Q19: Find the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find the

Q20: A conservation organization releases 20 wolves into

Q21: Match the logistic equation and initial condition

Q22: Find the orthogonal trajectories of the family

Q24: Which of the following is a solution

Q25: A conservation organization releases 30 panthers into

Q26: The half-life of the carbon isotope C-14

Q27: A calf that weighs 70 pounds at

Q28: Assume an object weighing 7 pounds is