Solved

A Ball Is Thrown Vertically Upwards from a Height of 8

Question 18

Multiple Choice

A ball is thrown vertically upwards from a height of 8 ft with an initial velocity of 30 ft per second. How high will the ball go? Note that the acceleration of the ball is given by A ball is thrown vertically upwards from a height of 8 ft with an initial velocity of 30 ft per second. How high will the ball go? Note that the acceleration of the ball is given by 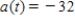feet per second per second. A) 18.5469 ft B) 34.1875 ft C) 53.1875 ft D) 50.1875 ft E) 22.0625 ft feet per second per second.


A) 18.5469 ft
B) 34.1875 ft
C) 53.1875 ft
D) 50.1875 ft
E) 22.0625 ft

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q13: Sketch the region whose area is given

Q14: Evaluate the definite integral. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q15: Find the sum given below. ​ <img

Q16: Find the average value of the function

Q17: Evaluate the limit <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Evaluate the

Q19: Find the indefinite integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find

Q20: Find the indefinite integral. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q21: Find the derivative of the function <img

Q22: Find the indefinite integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find

Q23: Find the derivative of the function <img