Solved

Find the X-Values (If Any) at Which the Function

Question 35

Multiple Choice

Find the x-values (if any) at which the function Find the x-values (if any) at which the function 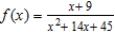is not continuous. Which of the discontinuities are removable? ​ A) no points of discontinuity B) x = -9 (not removable) , x = -5 (removable) C) x = -9 (removable) , x = -5 (not removable) D) no points of continuity E) x = -9 (not removable) , x = -5 (not removable) is not continuous. Which of the discontinuities are removable? ​


A) no points of discontinuity
B) x = -9 (not removable) , x = -5 (removable)
C) x = -9 (removable) , x = -5 (not removable)
D) no points of continuity
E) x = -9 (not removable) , x = -5 (not removable)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q9: Determine the following limit. (Hint: Use the

Q30: Complete the table and use the result

Q32: Find the limit. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find

Q33: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Let and

Q34: Find the constant a such that the

Q36: Find the vertical asymptotes (if any) of

Q37: Decide whether the following problem can be

Q38: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find where

Q39: Suppose that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Suppose that

Q40: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Let and