Solved

Let and Let S Be the Cylinder

Question 123

Multiple Choice

Let 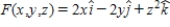Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E) and let S be the cylinder Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E) , Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E) Verify the Divergence Theorem by evaluating Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E) as a surface integral and as a triple integral. ​ Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E) ​


A) Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E)
B) Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E)
C) Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E)
D) Let and let S be the cylinder , Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. ​ ​ A) B) C) D) E)
E) Let and let S be the cylinder 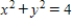, 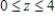Verify the Divergence Theorem by evaluating 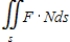as a surface integral and as a triple integral.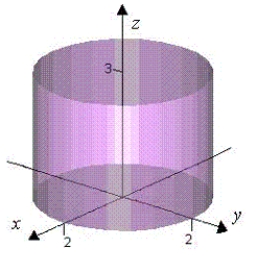 ​ ​ A) 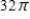B) C) 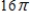D) 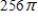E)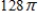

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q118: Find the value of the line integral

Q119: Find the area of the surface over

Q120: Use Green's Theorem to calculate the work

Q121: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Compute for

Q122: Verify Green's Theorem by evaluating both integrals

Q124: Use Divergence Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q125: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Evaluate where

Q126: Use a computer algebra system to evaluate

Q127: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Let and

Q128: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Evaluate ,