Solved

Combine the Sum of the Two Iterated Integrals into a Single

Question 82

Multiple Choice

Combine the sum of the two iterated integrals into a single integral by converting to polar coordinates. Evaluate the resulting iterated integral. Combine the sum of the two iterated integrals into a single integral by converting to polar coordinates. Evaluate the resulting iterated integral. A) B) C) D) E)


A) Combine the sum of the two iterated integrals into a single integral by converting to polar coordinates. Evaluate the resulting iterated integral. A) B) C) D) E)
B) Combine the sum of the two iterated integrals into a single integral by converting to polar coordinates. Evaluate the resulting iterated integral. A) B) C) D) E)
C) Combine the sum of the two iterated integrals into a single integral by converting to polar coordinates. Evaluate the resulting iterated integral. A) B) C) D) E)
D) Combine the sum of the two iterated integrals into a single integral by converting to polar coordinates. Evaluate the resulting iterated integral. A) B) C) D) E)
E) Combine the sum of the two iterated integrals into a single integral by converting to polar coordinates. Evaluate the resulting iterated integral. 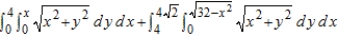A) 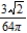B) 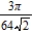C) 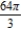D) 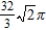E)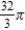

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q77: Use spherical coordinates to find the volume

Q78: Find the center of mass of the

Q79: Find the average value of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q80: Use spherical coordinates to find the z

Q81: Use cylindrical coordinates to find the mass

Q83: Find the area of the portion of

Q84: Find the area of the surface for

Q85: Find the area of the surface given

Q86: Set up and evaluate a double integral

Q87: Suppose the population density of a city