Solved

Determine the Interval on Which the Vector-Valued Function Is

Question 48

Multiple Choice

Determine the interval on which the vector-valued function Determine the interval on which the vector-valued function is continuous. A) B) C) D) E) is continuous.


A) Determine the interval on which the vector-valued function is continuous. A) B) C) D) E)
B) Determine the interval on which the vector-valued function is continuous. A) B) C) D) E)
C) Determine the interval on which the vector-valued function is continuous. A) B) C) D) E)
D) Determine the interval on which the vector-valued function is continuous. A) B) C) D) E)
E) Determine the interval on which the vector-valued function 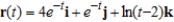is continuous. A) B) 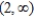C) 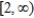D) 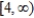E)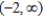

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q43: Find the length of the plane curve

Q44: Use the given acceleration function and initial

Q45: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find given

Q46: Sketch the curve represented by the vector-valued

Q47: The quarterback of a football team releases

Q49: Find the arc length for <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"

Q50: Use the properties of the derivative to

Q51: Suppose the two particles travel along the

Q52: The graph below is most likely the

Q53: Use the properties of the derivative to