Multiple Choice
Find the area of the surface generated by revolving the curve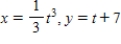 
about the y-axis on the interval 
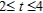. Round your answer to two decimal places.
A) 1436.54
B) 1413.69
C) 1401.46
D) 706.85
E) 2132.77
Correct Answer:
Verified
Correct Answer:
Verified
Related Questions
Q48: Find a set of parametric equations for
Q49: Find the arc length of the curve
Q50: Convert the rectangular equation to polar form.
Q51: Sketch the curve represented by the parametric
Q52: Find the second derivative <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Find
Q54: Convert the rectangular equation to polar form.
Q55: Find a set of parametric equations for
Q56: Identify any points at which the cycloid
Q57: Find a polar equation for the parabola
Q58: Find the center of the ellipse given