Solved

Find Two Solutions of the Equation

Question 105

Multiple Choice

Find two solutions of the equation. Give your answers in radians
(Find two solutions of the equation. Give your answers in radians ( ) . Do not use a calculator. ​ ​ A) B) C) D) E) ) . Do not use a calculator. ​ Find two solutions of the equation. Give your answers in radians ( ) . Do not use a calculator. ​ ​ A) B) C) D) E) ​


A) Find two solutions of the equation. Give your answers in radians ( ) . Do not use a calculator. ​ ​ A) B) C) D) E)
B) Find two solutions of the equation. Give your answers in radians ( ) . Do not use a calculator. ​ ​ A) B) C) D) E)
C) Find two solutions of the equation. Give your answers in radians ( ) . Do not use a calculator. ​ ​ A) B) C) D) E)
D) Find two solutions of the equation. Give your answers in radians ( ) . Do not use a calculator. ​ ​ A) B) C) D) E)
E) Find two solutions of the equation. Give your answers in radians (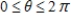 ) . Do not use a calculator.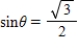 ​ ​ A) 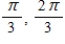B) 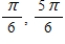C) 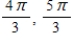D) 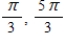E)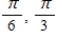

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q100: A moving conveyor is built to rise

Q101: Evaluate the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Evaluate the

Q102: A company reimburses its sales representatives <img

Q103: Sketch the line passing through the point

Q104: Use the result, "the line with intercepts

Q106: Determine whether the function is even, odd,

Q107: Use the functions <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg" alt="Use the

Q108: An open box of maximum volume is

Q109: Evaluate the sine, cosine, and tangent of

Q110: Determine the quadrant in which <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8527/.jpg"