Solved

Evaluate the Integral by Making an Appropriate Change of Variables

Question 36

Short Answer

Evaluate the integral by making an appropriate change of variables. Round your answer to two decimal places. Evaluate the integral by making an appropriate change of variables. Round your answer to two decimal places. R is the parallelogram bounded by the lines . R is the parallelogram bounded by the lines Evaluate the integral by making an appropriate change of variables. Round your answer to two decimal places. 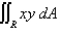R is the parallelogram bounded by the lines . .

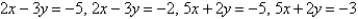Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q31: Use the transformation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg" alt="Use the

Q32: Use a triple integral to find the

Q33: Use polar coordinates to evaluate. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg"

Q34: Determine whether to use polar coordinates or

Q35: Find the mass of the solid S

Q37: Find the mass of the solid E,

Q38: Identify the surface with equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg"

Q39: Evaluate the double integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg" alt="Evaluate

Q40: Identify the surface with equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg"

Q41: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg" alt="Evaluate the