Solved

Find the Mass and the Center of Mass of the Lamina

Question 4

Multiple Choice

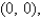
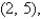Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , and Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , , and having the mass density Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) ,


A) Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , ,
Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) ,
B) Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , , Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) ,
C) Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , , Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) ,
D) Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) , ,
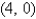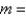
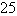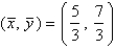
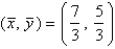
Find the mass and the center of mass of the lamina occupying the region R, where R is the triangular region with vertices and , and having the mass density A) , B) , C) , D) ,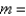

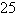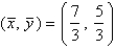
Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Evaluate the iterated integral by converting to

Q2: Find the volume under <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg" alt="Find

Q3: Use cylindrical or spherical coordinates, whichever seems

Q5: Sketch the solid whose volume is given

Q6: Evaluate the double integral by first identifying

Q7: Find the Jacobian of the transformation. <img

Q8: Use polar coordinates to find the volume

Q9: Evaluate the double integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg" alt="Evaluate

Q10: Evaluate the triple integral. Round your answer

Q11: Express the volume of the wedge in