Multiple Choice
A woman at a point A on the shore of a circular lake with radius 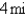 wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of
wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of  and row a boat at
and row a boat at 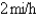 . How should she proceed? (Find
. How should she proceed? (Find 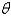 ) . Round the result, if necessary, to the nearest hundredth.
) . Round the result, if necessary, to the nearest hundredth. 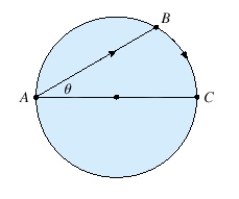
A) 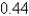 radians
radians
B) She should row from point A to point C radians
C) 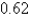 radians
radians
D) 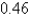 radians
radians
E) She should walk around the lake from point A to point C.
Correct Answer:

Verified
Correct Answer:
Verified
Q13: The graph of the derivative <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg"
Q14: A car braked with a constant deceleration
Q15: Find the number c that satisfies the
Q16: The function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg" alt="The function
Q17: Find the critical number(s), if any, of
Q19: Use the guidelines of this section to
Q20: Use Newton's method with the specified initial
Q21: Consider the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg" alt="Consider the
Q22: Given <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8390/.jpg" alt="Given .(a)
Q23: Use the guidelines of this section to