Solved

The Function Satisfies the Hypotheses of Rolle's Theorem on the Interval

Question 53

Multiple Choice

The function 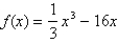The function satisfies the hypotheses of Rolle's Theorem on the interval . Find all values of c that satisfy the conclusion of the theorem. A) B) C) D) satisfies the hypotheses of Rolle's Theorem on the interval The function satisfies the hypotheses of Rolle's Theorem on the interval . Find all values of c that satisfy the conclusion of the theorem. A) B) C) D) . Find all values of c that satisfy the conclusion of the theorem.


A) The function satisfies the hypotheses of Rolle's Theorem on the interval . Find all values of c that satisfy the conclusion of the theorem. A) B) C) D)
B) The function satisfies the hypotheses of Rolle's Theorem on the interval . Find all values of c that satisfy the conclusion of the theorem. A) B) C) D)
C) The function satisfies the hypotheses of Rolle's Theorem on the interval . Find all values of c that satisfy the conclusion of the theorem. A) B) C) D)
D) The function satisfies the hypotheses of Rolle's Theorem on the interval 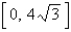. Find all values of c that satisfy the conclusion of the theorem. A) 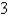B) C) 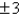D)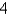

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q48: Verify that the function satisfies the three

Q49: Find all the critical numbers of the

Q50: At 4:00 P.M. a car's speedometer reads

Q51: Use the guidelines of this section to

Q52: Find the absolute maximum and absolute minimum

Q54: Find an equation of the line through

Q55: Find the critical number(s), if any, of

Q56: Use the guidelines of this section to

Q57: Use Newton's method to approximate the given

Q58: Find the critical number(s), if any, of