Multiple Choice
Use an inverse function to write as a function of x. 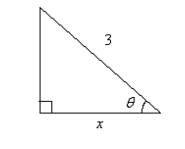
A) 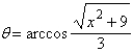
B) 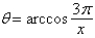
C) 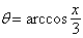
D) 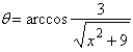
E) 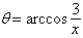
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q8: Determine the quadrant in which a 130°
Q41: Determine the quadrant in which an
Q42: Use a calculator to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8632/.jpg"
Q43: Determine the quadrant in which a <img
Q44: Rewrite <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8632/.jpg" alt=" Rewrite
Q47: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8632/.jpg" alt="If and
Q48: Given the figure below, determine the value
Q49: Find (if possible) the complement of <img
Q50: Convert <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8632/.jpg" alt="Convert to
Q51: Determine the quadrant in which a <img