Solved

Let F (X) = 2x - 1, G(x) = 3x

Question 63

Multiple Choice

Let f (x) = 2x - 1, g(x) = 3x - 2. Find the domain of the function. Let f (x) = 2x - 1, g(x) = 3x - 2. Find the domain of the function. A) B) C) D) E)


A) Let f (x) = 2x - 1, g(x) = 3x - 2. Find the domain of the function. A) B) C) D) E)
B) Let f (x) = 2x - 1, g(x) = 3x - 2. Find the domain of the function. A) B) C) D) E)
C) Let f (x) = 2x - 1, g(x) = 3x - 2. Find the domain of the function. A) B) C) D) E)
D) Let f (x) = 2x - 1, g(x) = 3x - 2. Find the domain of the function. A) B) C) D) E)
E) Let f (x) = 2x - 1, g(x) = 3x - 2. Find the domain of the function. A) 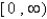B) 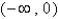C) 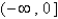D) E)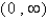

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q45: Find the slope of the line through

Q58: Tell where the function is decreasing. <img

Q59: Find the inverse of the one-to-one function.

Q60: Determine whether the function is one-to-one. <img

Q62: Find the inverse of the one-to-one function.

Q64: Evaluate the difference quotient for the function.

Q65: Find the graph of the equation. <img

Q67: Which graph represents the function? g(x) =

Q68: Graph the piecewise-defined function. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8632/.jpg" alt="Graph

Q84: Find the slope of the line through