Solved

Use the Principle of Mathematical Induction to Find the Equivalent

Question 12

Multiple Choice

Use the principle of mathematical induction to find the equivalent expression for every positive integer n. Use the principle of mathematical induction to find the equivalent expression for every positive integer n. A) B) C) D) E)


A) Use the principle of mathematical induction to find the equivalent expression for every positive integer n. A) B) C) D) E)
B) Use the principle of mathematical induction to find the equivalent expression for every positive integer n. A) B) C) D) E)
C) Use the principle of mathematical induction to find the equivalent expression for every positive integer n. A) B) C) D) E)
D) Use the principle of mathematical induction to find the equivalent expression for every positive integer n. A) B) C) D) E)
E) Use the principle of mathematical induction to find the equivalent expression for every positive integer n. 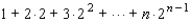A) B) C) 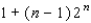D) 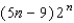E)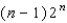

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q7: In a round-robin tennis tournament, every player

Q8: To win a state lottery game, a

Q9: Find the third term of the sequence:

Q10: Use the binomial theorem to expand and

Q11: A rubber ball is dropped from a

Q13: Find the third term of the recursively

Q14: Use the principle of mathematical induction to

Q15: If seven basketball teams are in a

Q16: A bicycle rider coasts downhill, traveling 7

Q17: Find the nth term and the fifth