Solve the Problem $149 \mathrm {~km}$ Determine an Equation for the Ellipse If the Distance

Multiple Choice

Solve the problem.
-A satellite is to be put into an elliptical orbit around a moon. The moon is a sphere with radius of $149 \mathrm {~km}$ . Determine an equation for the ellipse if the distance of the satellite from the surface of the moon varies from 910 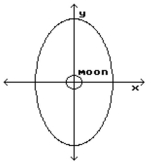$\mathrm { km }$ to $488 \mathrm {~km}$ .

A) $\frac { x ^ { 2 } } { 10592 } + \frac { y ^ { 2 } } { 637 ^ { 2 } } = 1$
B) $\frac { x ^ { 2 } } { 488 } + \frac { y ^ { 2 } } { 910 } = 1$
C) $\frac { x ^ { 2 } } { 637 ^ { 2 } } + \frac { y ^ { 2 } } { 10592 } = 1$
D) $\frac { x ^ { 2 } } { 910 } + \frac { y ^ { 2 } } { 488 } = 1$