Multiple Choice
Choose the graph which matches the function.
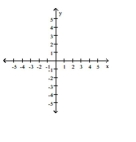
- 
A) 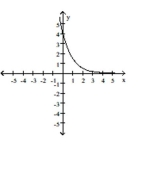
B) 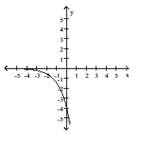
C) 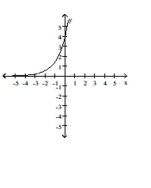
D) 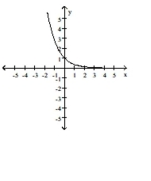
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q302: Write the expression using only the
Q303: Assuming all variables are positive, use properties
Q304: Find the amount accumulated after investing a
Q305: Graph the function. Describe its position
Q306: Solve the problem.<br>-Find the present value of
Q308: Determine a formula for the exponential
Q309: Solve the problem.<br>-The number of bacteria
Q310: Solve the problem.<br>-Find a natural logarithmic
Q311: Graph the function. Describe its position
Q312: Solve the problem.<br>-If x is the hydrogen