Multiple Choice
Solve the problem.
-Use the data in the table to compute a logistic regression model for the population of the city t years after 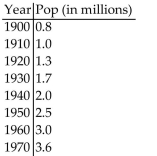
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q116: Evaluate the logarithm.<br>- <span class="ql-formula" data-value="\log
Q117: Solve the problem.<br>-The number of books
Q118: Assuming all variables are positive, use properties
Q119: Solve the problem.<br>-Find the interest rate necessary
Q120: Solve the problem.<br>-There are currently 57
Q122: Solve the problem.<br>-The table shows the
Q123: Describe how to transform the graph
Q124: Graph the function and analyze it for
Q125: Find the amount accumulated after investing a
Q126: Graph the function and analyze it for