Multiple Choice
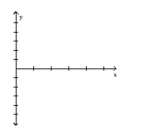
Match the equation to one of the curves (for x ≥ 0) .
- 
A) 
B) 
C) 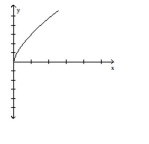
D) 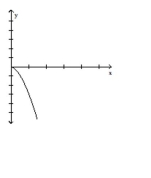
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q387: Using the given zero, find all
Q388: Write an equation for the quadratic
Q389: Determine if the function is a
Q390: Match the equation to one of
Q391: Determine whether the power function is
Q393: Find all of the real zeros
Q394: If the following is a polynomial
Q395: Graph the function in a viewing
Q396: Solve the inequality.<br>- <span class="ql-formula" data-value="(
Q397: Solve the problem.<br>-The length of a