Multiple Choice
Match the equation to one of the curves (for x ≥ 0) .
- 
A) 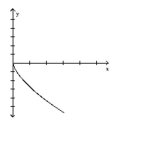
B) 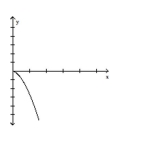
C) 
D) 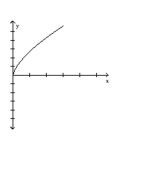
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q319: Match the graph of the rational
Q320: Use a graphing calculator to approximate
Q321: Find all rational zeros.<br>- <span class="ql-formula"
Q322: Find the remainder when f(x) is
Q323: Choose the one alternative that best
Q325: Find the requested function.<br>-Find the cubic
Q326: Solve the inequality.<br>- <span class="ql-formula" data-value="3
Q327: Find the vertex of the graph
Q328: State the power and constant of
Q329: Solve the problem.<br>-Find the remainder when