Multiple Choice
Use limits to describe the behavior of the rational function near the indicated asymptote.
-
Describe the behavior of the function near its horizontal asymptote (the end behavior) .
A)
B)
C) 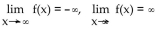
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q170: Write the polynomial in standard form
Q171: Solve the problem.<br>-The first column shows
Q172: Provide an appropriate response.<br>-Fill in the
Q173: Solve the problem.<br>-Dan's long-distance phone carrier
Q174: For the given function, find all
Q176: Determine the x values that cause
Q177: List the x- and y-intercepts, and
Q178: Divide f(x) by d(x), and write
Q179: Write the word or phrase that
Q180: Solve the problem.<br>-The stadium vending company