Multiple Choice
Solve the problem.
-The function
gives the body concentration , in parts per million, of a certain dosage of medication after time , in hours.
Graph the function on the interval and complete the following:
as
A) 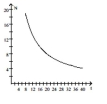
as
B) 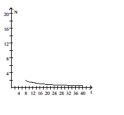
as
C) 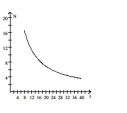
as
D) 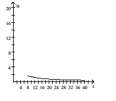
as ,
Correct Answer:

Verified
Correct Answer:
Verified
Q397: Solve the problem.<br>-The length of a
Q398: For the given function, find all
Q399: Choose the one alternative that best
Q400: Graph the function.<br>- <span class="ql-formula" data-value="f(x)=(x-1)(x+3)^{4}"><span
Q401: Determine whether the power function is
Q403: For the given function, find all
Q404: Provide an appropriate response.<br>-Suppose that a
Q405: Divide f(x) by d(x), and write
Q406: Using the given zero, find all
Q407: Data are given for y as