Multiple Choice
Solve the problem.
-The population , in thousands, of Jonesburg is given by
where is the time, in months.
Graph the function on the interval and complete the following: as
A) 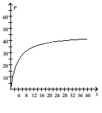
as .
B) 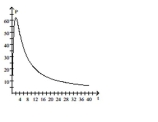
as
C) 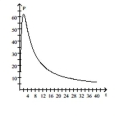
as
D) 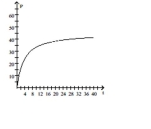
as .
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q253: Write a linear factorization of the
Q254: Choose the one alternative that best
Q255: Write a linear factorization of the
Q256: Solve the problem.<br>-The Cool Company determines
Q257: Solve the inequality.<br>- <span class="ql-formula" data-value="\frac
Q259: Find all of the real zeros
Q260: State how many complex and real
Q261: Solve the problem.<br>- <span class="ql-formula" data-value="\mathrm
Q262: State the power and constant of
Q263: Write the statement as a power