Multiple Choice
Match the equation with the appropriate graph.
-
A) 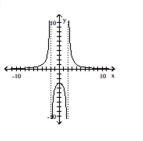
B) 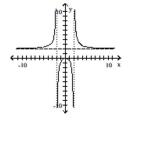
C) 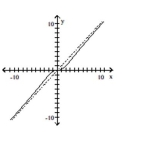
D) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q162: Identify which of the twelve basic
Q163: Tell which of the following types of
Q164: Sketch the graph of y1 as
Q165: Tell which of the following types of
Q166: Determine if the function is one-to-one.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8181/.jpg"
Q168: Solve the problem.<br>-A rock is thrown
Q169: Give the equation of the function
Q170: Find the range of the function.<br>-
Q171: Match the equation with the appropriate
Q172: Identify intervals on which the function