Solved

If the Sample Size Is Large (N ≥ 30), Then

Question 28

Multiple Choice

If the sample size is large (n ≥ 30) , then, regardless of the population distribution, which of the following summarizes the sampling distribution of random variable If the sample size is large (n ≥ 30) , then, regardless of the population distribution, which of the following summarizes the sampling distribution of random variable ? A) B) C) D) ?


A) If the sample size is large (n ≥ 30) , then, regardless of the population distribution, which of the following summarizes the sampling distribution of random variable ? A) B) C) D)
B) If the sample size is large (n ≥ 30) , then, regardless of the population distribution, which of the following summarizes the sampling distribution of random variable ? A) B) C) D)
C) If the sample size is large (n ≥ 30) , then, regardless of the population distribution, which of the following summarizes the sampling distribution of random variable ? A) B) C) D)
D) If the sample size is large (n ≥ 30) , then, regardless of the population distribution, which of the following summarizes the sampling distribution of random variable 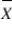? A) 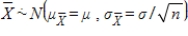B) 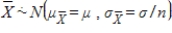C) 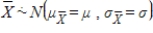D)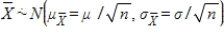

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q23: If the monthly rents of all one-bedroom

Q24: Suppose we know that the proportion of

Q25: A _ is any quantity computed from

Q26: Homeowners who recently bought their houses from

Q27: All statistics may be treated as:<br>A) characteristics

Q29: Concerning the sampling distribution of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB8195/.jpg"

Q30: It is believed that 15% of people

Q31: What effect does increasing the sample size

Q32: According to the Central Limit Theorem, as

Q33: To better understand the student body, a