TABLE 13-11 A Weight-Loss Clinic Wants to Use Regression Analysis to Build

Multiple Choice

TABLE 13-11
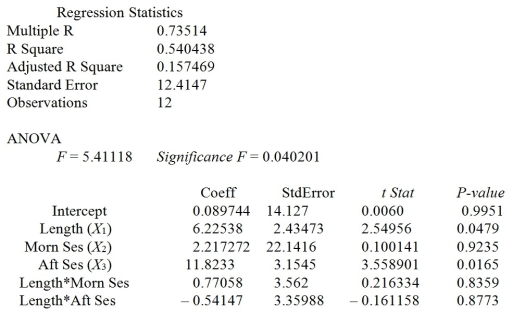
A weight-loss clinic wants to use regression analysis to build a model for weight loss of a client (measured in pounds) . Two variables thought to affect weight loss are client's length of time on the weight loss program and time of session. These variables are described below:
Y = Weight loss (in pounds)
X1 = Length of time in weight-loss program (in months)
X2 = 1 if morning session, 0 if not
X3 = 1 if afternoon session, 0 if not (Base level = evening session)
Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
Y = β0 + β1X1 + β2X2 + β3X3 + β4X1X2 + β5X1X3 + ε
Partial output from Microsoft Excel follows:

-In a multiple regression model, the adjusted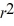

A) cannot be negative.
B) can sometimes be negative.
C) can sometimes be greater than +1.
D) has to fall between 0 and +1.