TABLE 13-15 the Superintendent of a School District Wanted to Predict the Predict

Multiple Choice

TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing) , daily mean of the percentage of students attending class (% Attendance) , mean teacher salary in dollars (Salaries) , and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, 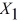= : % Attendance, 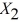= Salaries and 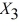= Spending:

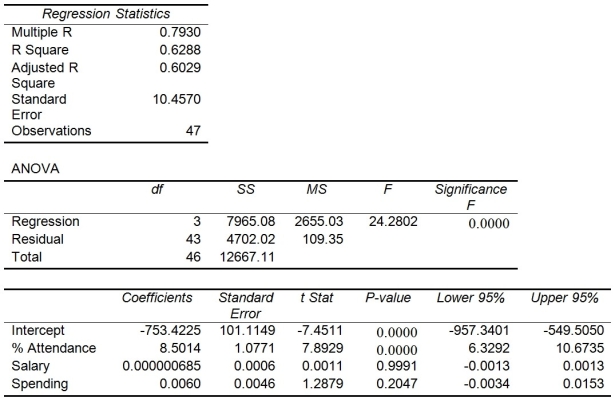
-Referring to Table 13-15, which of the following is a correct statement?

A) 62.88% of the total variation in the percentage of students passing the proficiency test can be explained by daily mean of the percentage of students attending class, mean teacher salary, and instructional spending per pupil.
B) 62.88% of the total variation in the percentage of students passing the proficiency test can be explained by daily mean of the percentage of students attending class, mean teacher salary, and instructional spending per pupil, after adjusting for the number of predictors and sample size.
C) 62.88% of the total variation in the percentage of students passing the proficiency test can be explained by daily mean of the percentage of students attending class, holding constant the effect of mean teacher salary and instructional spending per pupil.
D) 62.88% of the total variation in the percentage of students passing the proficiency test can be explained by daily mean of the percentage of students attending class, after adjusting for the effect of mean teacher salary and instructional spending per pupil.