Multiple Choice
Suppose the gravitational force of the Earth on a body was 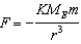 . What escape velocity ve would a body need to escape the gravitational field of the Earth?
. What escape velocity ve would a body need to escape the gravitational field of the Earth?
A) .
B) .
C) .
D) .
E) .
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q3: What is the gravitational force on a
Q5: When two solid spheres of the same
Q7: The figure below shows a planet travelling
Q8: A satellite circles planet Roton every 2.8
Q9: A satellite of mass m circles
Q10: Refer to Exhibit 11-1 below.Exhibit 11-1 Three
Q34: Two identical planets orbit a star in
Q36: What is the period of revolution of
Q38: When a falling meteor is at a
Q47: A spaceship of mass m circles a