Multiple Choice
Which of the following products of ratios gives the conversion factors to convert metres per second to parsecs per year ? A parsec is a unit of distance used in astrophysics, and is equal to 3.26 light years. A light year is 9.46 x 1015 m.
A)
B)
C) 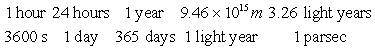
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q9: A rectangle has a length of 1.323
Q11: You are trying to compare the fuel
Q11: The density of an object is defined
Q12: Which one of the quantities below
Q12: One number has three significant figures and
Q13: The term <span class="ql-formula" data-value="\frac{1}{2}
Q14: Five people measure the length of a
Q15: Two rocket engineers are trying to see
Q18: Spike claims that dimensional analysis shows
Q21: Which quantity can be converted to