Multiple Choice
light on top of the car turns at a rate of revolution per second. The rate at which the light beam moves along the wall is . Find the limit of as .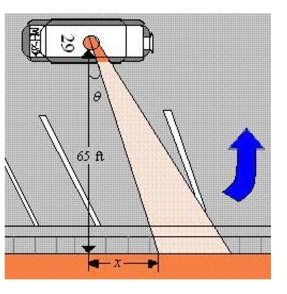
A)
B)
C) 0
D) 65
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q20: <span class="ql-formula" data-value="\text { Consider the function
Q21: Decide whether the following problem can
Q22: Complete the table and use the
Q23: Find the limit. <span class="ql-formula"
Q24: <span class="ql-formula" data-value="\text { Consider the function
Q26: Find the limit (if it exists).
Q27: <span class="ql-formula" data-value="\text { Find the limit
Q28: Determine the following limit. (Hint: Use
Q29: <span class="ql-formula" data-value="\text { Let } f
Q30: <span class="ql-formula" data-value="\text { Find all the