Multiple Choice
Sketch the curve represented by the parametric equations, and write the corresponding rectangular equation by eliminating the parameter.
A) 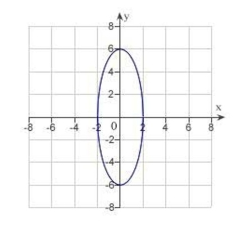
B) 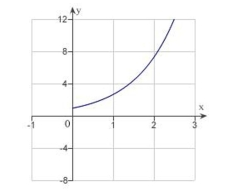
C) 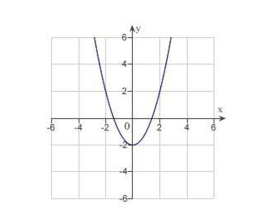
D) 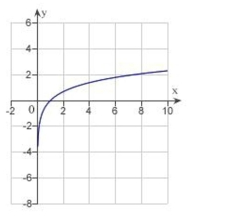
E) 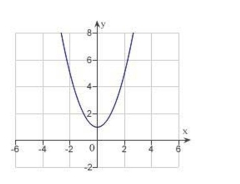
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q12: <span class="ql-formula" data-value="\text { Identify the conic
Q13: Find a set of parametric equations
Q14: <span class="ql-formula" data-value="\text { Identify the graph
Q15: <span class="ql-formula" data-value="\text { Identify any points
Q16: Find an equation of the tangent
Q18: Find a polar equation for the
Q19: Find the eccentricity and distance from
Q20: <span class="ql-formula" data-value="\text { Find } \frac
Q21: Find the points of intersection of
Q22: Classify the graph of the equation