The Parametric Equations for the Path of a Projectile Launched $\theta$

Multiple Choice

The parametric equations for the path of a projectile launched at a height h feet above the ground, at an angle $\theta$ with the horizontal and having an initial velocity of $v _ { 0 }$ feet per second is given by $x = \left( v _ { 0 } \cos \theta \right) t$ and $y = h + \left( v _ { 0 } \sin \theta \right) t - 16 t ^ { 2 }$ . The center field fence in a ballpark is 10 feet high and 400 feet from home plate. The ball is hit 2 feet above the ground. It leaves the bat at an angle of $\theta$ degrees with the horizontal at a speed of 100 miles per hour as shown in the figure. Write a set of parametric equations for the path of the ball.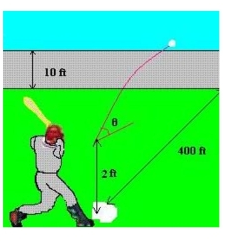

A) $x = \left( \frac { 440 } { 3 } \cos \theta \right) t , y = 2 + \left( \frac { 440 } { 3 } \sin \theta \right) t$
B) $x = 2 + \left( \frac { 440 } { 3 } \sin \theta \right) t , y = \left( \frac { 440 } { 3 } \cos \theta \right) t$
C) $x = 2 + \left( \frac { 440 } { 3 } \sin \theta \right) t - 16 t ^ { 2 } , y = \left( \frac { 440 } { 3 } \cos \theta \right) t$
D) $x = \left( \frac { 440 } { 3 } \sin \theta \right) t , y = 2 + \left( \frac { 440 } { 3 } \cos \theta \right) t - 16 t ^ { 2 }$
E) $x = \left( \frac { 440 } { 3 } \cos \theta \right) t , y = 2 + \left( \frac { 440 } { 3 } \sin \theta \right) t - 16 t ^ { 2 }$