Multiple Choice
Write an integral that represents the area of the shaded region for shown in the figure. Do not evaluate the integral. 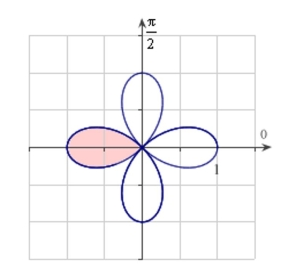
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q23: Find the vertices of the ellipse
Q24: Find all points (if any) of
Q25: Find a polar equation for the
Q26: Match the equation with its graph.
Q27: Find the eccentricity of the polar
Q29: <span class="ql-formula" data-value="\text { Find the second
Q30: Find the length of the curve
Q31: Match the equation with its graph.
Q32: Sketch the curve represented by the
Q33: <span class="ql-formula" data-value="\text { Determine the }