Multiple Choice
Examine the function 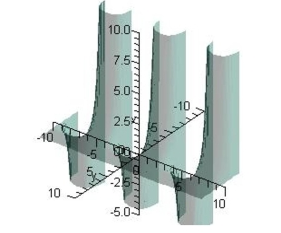
A) saddle point:
B) relative minimum:
C) relative maximum:
D) relative minimum:
E) no critical points
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q112: <span class="ql-formula" data-value="\text { Find } \frac
Q113: Sketch the surface given by the
Q114: Use polar coordinates and L'Hopital's Rule
Q115: Find the limit. <span class="ql-formula"
Q116: Determine the continuity of the function
Q118: <span class="ql-formula" data-value="\text { For } f
Q119: Find the least squares regression line
Q120: Find the least squares regression line
Q121: The surface of a mountain is
Q122: <span class="ql-formula" data-value="\text { Find } \frac