Compare the Right-Hand and Left-Hand Derivatives to Determine Whether or Not

Multiple Choice

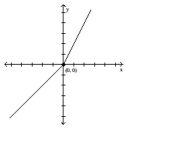
Compare the right-hand and left-hand derivatives to determine whether or not the function is differentiable at the point whose coordinates are given.
- $$y = x \quad y = 2 x$$

A) Since $\lim _ { x \rightarrow0 ^ { + } } f ^ { \prime } ( x ) = - 2$ while $\lim _ { x \rightarrow 0 ^ { - } } f ^ { \prime } ( x ) = - 1 , f ( x )$ is not differentiable at $x = 0$ .
B) Since $\lim _ { x \rightarrow0 ^ { + } } f ^ { \prime } ( x ) = 2$ while $\lim _ { x \rightarrow - ^ { - } } f ^ { \prime } ( x ) = 1 , f ( x )$ is not differentiable at $x = 0$ .
C) Since $\lim _ { x \rightarrow 0^ { + } } f ^ { \prime } ( x ) = 1$ while $\lim _ { x - \theta ^ { - } } f ^ { \prime } ( x ) = 2 , f ( x )$ is not differentiable at $x = 0$ .
D) Since $\lim _ { x \rightarrow0^ { + } } f ^ { \prime } ( x ) = 1$ while $\lim _ { x - \theta ^ { - } } f ^ { \prime } ( x ) = 1 , f ( x )$ is differentiable at $x = 0$ .