Graph the Function $y=(-x)^{5 / 2}$ A) Decreasing $- \infty < x < \infty$

Multiple Choice

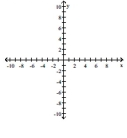
Graph the function. Specify the intervals over which the function is increasing and the intervals where it is decreasing.
- $y=(-x) ^{5 / 2}$

A) Decreasing 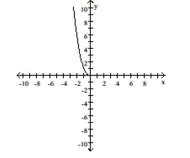$- \infty < x < \infty$

B) Decreasing $- \infty < x \leq 0$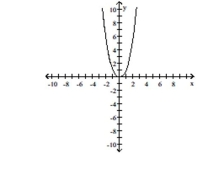
Increasing $0 \leq x < \infty$

C) Decreasing 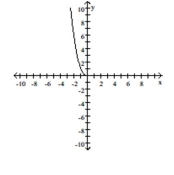$- \infty < x \leq 0$

D) Increasing $0 \leq x < \infty$