Multiple Choice
Approximate the solutions of the equation by considering its graph below. Round your answer to one decimal.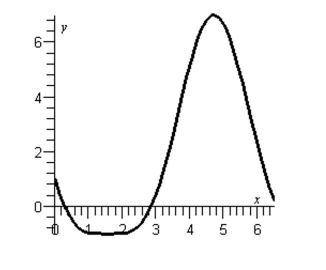
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q23: Verify the given identity.<br> <span class="ql-formula"
Q24: Which of the following is a
Q25: Find the exact value of
Q26: Use a double angle formula to
Q27: Find the exact value of
Q29: Use the figure below to find
Q30: Expand the expression below and use
Q31: Use the graph of the function
Q32: Use the half-angle formulas to determine
Q33: Determine which of the following are