Multiple Choice
Determine a piecewise-defined function for the graph shown below.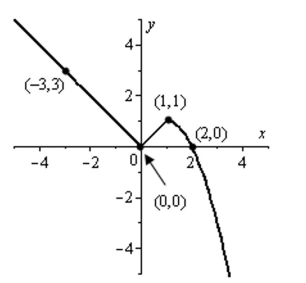
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q24: Algebraically determine whether the function below
Q25: Find the difference quotient and simplify
Q26: Find <span class="ql-formula" data-value="f \circ
Q27: Find the inverse function of
Q28: Evaluate the following function for
Q30: Decide whether the two functions shown in
Q31: Find the domain of the function.<br>
Q32: If f is an even function,
Q33: Find <span class="ql-formula" data-value="f \circ
Q34: Find <span class="ql-formula" data-value="( f