Multiple Choice
Find the inverse of . Then sketch the graphs of and on the same set of axes.
A)
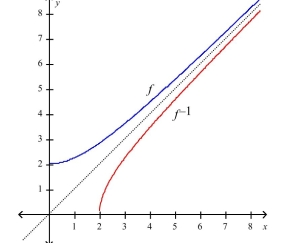
B)
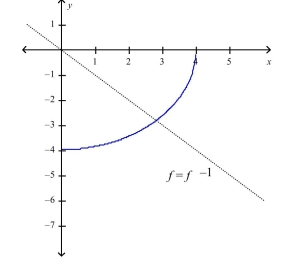
C) 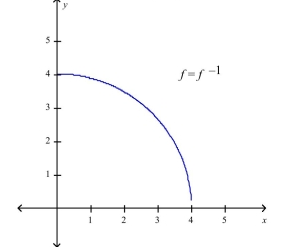
D) 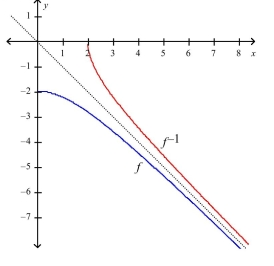
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q25: Find the limit.<br> <span class="ql-formula" data-value="\lim
Q26: Solve each equation for x. <br>(a)
Q27: Differentiate the function. <span class="ql-formula"
Q28: Evaluate the expression. <span class="ql-formula"
Q29: A painting in an art gallery
Q31: Find the solution of the equation
Q32: Find <span class="ql-formula" data-value="g ^
Q33: Evaluate the integral to three decimal
Q34: <span class="ql-formula" data-value="\text { Find the values
Q35: Suppose <span class="ql-formula" data-value="g"><span class="katex"><span