Multiple Choice
Solve the inequality and graph the solution on the real number line.
A) 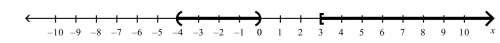
B) 
C) 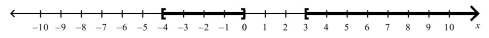
D) 
E) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q115: Simplify the rational expression, <span
Q116: Write the complex conjugate of the
Q117: Select the graph of the function
Q118: Use the position equation <span
Q119: Select the graph of the function
Q121: Identify all intercepts of <span
Q122: Use the position equation <span
Q123: Select the graph of the function
Q124: Select the correct graph of the
Q125: Solve the equation and write complex