Multiple Choice
Find the exact values of the three trignometric functions of the angle shown in the figure. (Use the Pythagorean Theorem to find the third side of the traingle.) 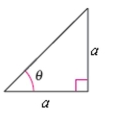
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q14: State the period of the function.
Q15: Use a calculator to evaluate the
Q16: Find an algebraic expression that is
Q17: The angle of elevation of the
Q18: Find the radian measure of the
Q20: Describe the behavior of the function
Q21: Write an equation for the function
Q22: An engineer erects a <span
Q23: For a person at rest, the
Q24: Find the values of <span