Multiple Choice
Find the standard form of the equation of the ellipse with the given characteristics and center at the origin. 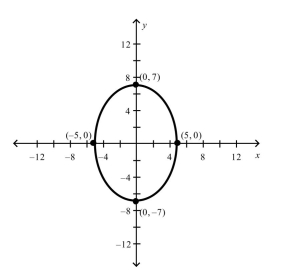
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q28: Convert the polar equation to rectangular
Q29: Find a polar equation of the
Q30: Find the standard form of the
Q31: Consider a line with slope m
Q32: Find the standard form of the
Q34: Find the inclination <span class="ql-formula"
Q35: Select the polar equation with graph.
Q36: Select the graph of the following
Q37: Identify the conic and select its
Q38: Eliminate the parameter and write the