Short Answer
Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal.
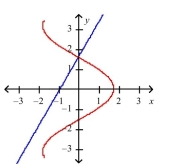
Correct Answer:

Verified
The curves...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q33: Differentiate.<br> <span class="ql-formula" data-value="y = \frac
Q34: The point <span class="ql-formula" data-value="P
Q35: <span class="ql-formula" data-value="\text { Let } f
Q36: The volume of a right circular
Q37: <span class="ql-formula" data-value="\text { Use the graph
Q39: Find the point at which the
Q40: Find the limit. <span class="ql-formula"
Q41: If a ball is thrown into
Q42: Find an expression for the function
Q43: Find the derivative of the function.<br>