Multiple Choice
Find the dimensions of the rectangle enclosed in the semicircle with the largest possible area.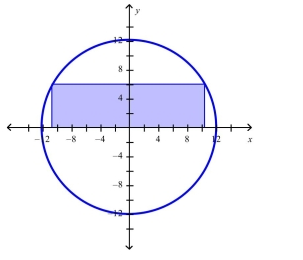
A) 5 in. in.
B) 6 in. in.
C) in. in.
D) in. in.
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q27: <span class="ql-formula" data-value="\text { What is the
Q28: A fence <span class="ql-formula" data-value="10
Q29: Given <span class="ql-formula" data-value="f (
Q30: For what values of <span
Q31: Find the critical numbers of
Q33: The graph of the derivative
Q34: Find the maximum area of a
Q35: The size of the monthly repayment
Q36: Sketch the graph of the function
Q37: Determine where the graph of the