Multiple Choice
The value for which Newton's method fails for the function below is shown in the graph. Give the reason why the method fails. 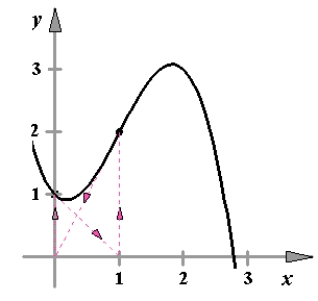
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q58: A Taylor polynomial approximation of
Q59: Find the radius of convergence of
Q60: Approximate the sum of the convergent
Q61: Differentiate the series for <span
Q62: Write an expression for the apparent
Q64: Bouncing Ball. A ball dropped from
Q65: Determine the convergence or divergence of
Q66: You are in a boat 2 miles
Q67: Determine whether the series <span
Q68: Determine the convergence or divergence of