Multiple Choice
Sketch a graph of a function f having the following characteristics.
A) 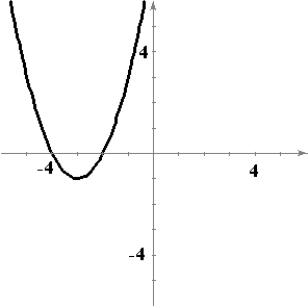
B) 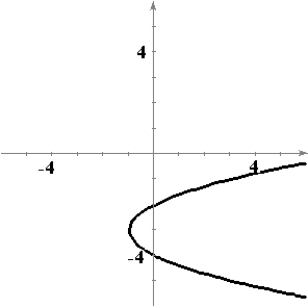
C) 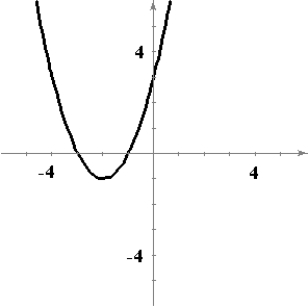
D) 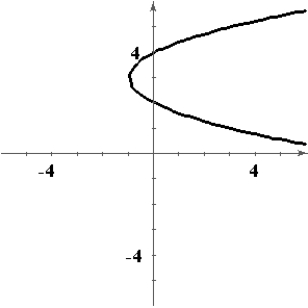
E) 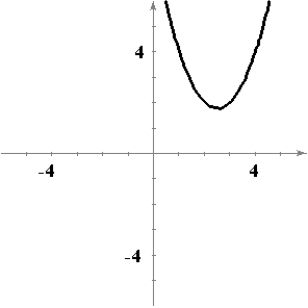
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q10: The profit P (in thousands of
Q11: Medication. The number of milligrams x
Q12: A retail sporting goods store estimates
Q13: Find the open intervals on which
Q14: Area. The radius, r, of a
Q16: Find the points of inflection and
Q17: Find all relative maxima of the
Q18: Find all relative extrema of the
Q19: Use the graph of <span
Q20: Let x represent the units of