Essay
The switch in the circuit shown below has been closed for a long time before it is opened at t . Find the voltage across the capacitor for . Assume . 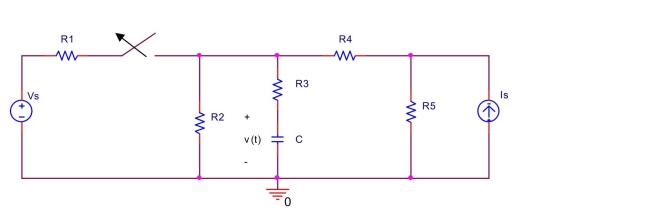
Correct Answer:

Verified
\[\begin{array} { l }
R _ { a } = R _ {...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
\[\begin{array} { l }
R _ { a } = R _ {...
R _ { a } = R _ {...
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Related Questions
Q4: the switch in the circuit shown
Q5: switch in the circuit shown below
Q6: The switch in the circuit shown
Q7: the switch in the circuit shown
Q8: the switch in the circuit shown
Q9: The switch in the circuit shown
Q11: The switch in the circuit shown
Q12: the switch in the circuit shown
Q13: The switch in the circuit shown
Q14: The switch in the circuit shown