Multiple Choice
A one-to-one function f is given. and graph fwith a solid line and with a dotted line on the same axes.
- 
A) 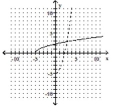
B) 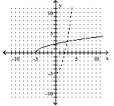
C) 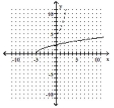
D) 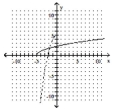
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q152: Determine whether the given functions are
Q153: Determine whether the function is a
Q154: Graph the function.<br>- <span class="ql-formula" data-value="f
Q155: For the given function, find the
Q156: Determine whether the given functions are
Q158: Evaluate.<br>-log9 81<br>A)81<br>B)4<br>C)9<br>D)2
Q159: Use properties of logarithms to expand
Q160: Evaluate.<br>- <span class="ql-formula" data-value="\log _ {
Q161: Find the unknown value.<br>- <span class="ql-formula"
Q162: Graph the function.<br>- <span class="ql-formula" data-value="f