Solve the Problem $\mathrm { d } = \sqrt { \mathrm { L } ^ { 2 } + \mathrm { W } ^ { 2 } + \mathrm { H } ^ { 2 } } ,$

Multiple Choice

Solve the problem.
-A formula for the length of a diagonal from the upper corner of a box to the opposite lower corner is $\mathrm { d } = \sqrt { \mathrm { L } ^ { 2 } + \mathrm { W } ^ { 2 } + \mathrm { H } ^ { 2 } } ,$ where L, W, and H are the length, width, and height, respectively. Find the length of t where L, W, and H are the length, width, and height, respectively. Find the length of the diagonal of the box if the length is 22 inches, width is 15 inches, and height is 6 inches. Leave your answer in
Simplified radical form.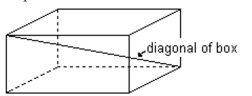

A) $\sqrt { 86 } \mathrm { ~in. }$
B) $\sqrt { 43 } \text { in. }$
C) $\sqrt { 745 } \text { in. }$
D) $\sqrt { 1490 } \text { in. }$